10.6.0.3 Tangent Space

Recall that the bump map normal $\vec{N'}$ is formed by $\vec{Pu} \times \vec{Pv}$. Assume that the surface $P$ is coincident with the $XY$ plane and that changes in $u$ and $v$ correspond to changes in $X$ and $Y$, respectively. Then $F$ can be substituted for $P'$, resulting in the following expression for the vector $N'$:

$$N' = \pmatrix{ -\frac{\partial F}{\partial u} \cr -\frac{\partial F}{\partial v} \cr 1 \cr }$$

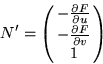
In order to evaluate the lighting equation, $N'$ must be normalized. If the displacements in the bump map are restricted to small values, however, the length of $N'$ will be so close to one as to be approximated by one. Then $N'$ itself can be substituted for $\vec{N}$ without normalization. If the diffuse intensity component $\vec{N} \cdot \vec{L}$ of the lighting equation is evaluated with the value presented above for $N'$, the result is the following:

$$N' \cdot L = - \frac{\partial F}{\partial u}L_x - \frac{\partial F}{\partial v}L_y + L_z$$ (1)

This expression requires the surface to lie in the $XY$ plane and that the $u$ and $v$ parameters change in $X$ and $Y$, respectively. Most surfaces, however, will have arbitrary locations and orientations in space. In order to use this simplification to perform bump mapping, the view direction $\vec{V}$, and light source direction $\vec{L}$ are transformed into tangent space.

Tangent space has 3 axes, $\vec{T}$, $\vec{B}$ and $\vec{N}$. The tangent vector, $\vec{T}$, is parallel to the direction of increasing $s$ on the surface. The normal vector, $\vec{N}$, is perpendicular to the surface. The binormal, $\vec{B}$, is perpendicular to both $\vec{N}$ and $\vec{T}$, and like $\vec{T}$, lies in the plane tangent to the surface. These vectors form a coordinate system that is attached to and varies over the surface.

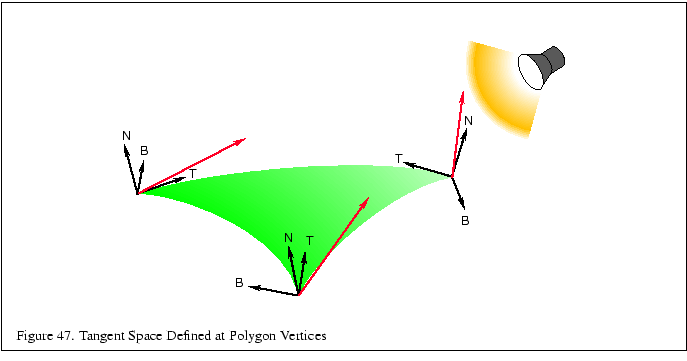
The light source is transformed into tangent space at each vertex of the polygon. To find the tangent space vectors at a vertex, use the vertex normal for $\vec{N}$ and find the tangent axis $\vec{T}$ by finding the vector direction of increasing $s$ in the object's coordinate system. The direction of increasing $t$ may also be used. Find $\vec{B}$ by computing the cross product of $\vec{N}$ and $\vec{T}$. These unit vectors form the transformation shown below:

$$\pmatrix{x' \cr y' \cr z\lq \cr w\lq \cr} = \pmatrix{ T_x & T_y ... ...V_z \cr 0 & 0 & 0 & 1 \cr } \pmatrix{ x \cr y \cr z \cr w \cr}$$ (2)

This transformation brings coordinates into tangent space, where the plane tangent to the surface lies in the $X-Y$ plane, and the normal to the surface coincides with the $Z$ axis. Note that the tangent space transformation varies for vertices representing a curved surface, and so this technique makes the approximation that curved surfaces are flat and the tangent space transformation is interpolated from vertex to vertex.