4.4 Image Tiling

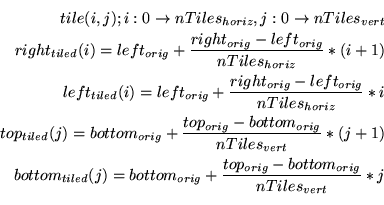
When rendering a scene in OpenGL, the resolution of the image is normally limited to the workstation screen size. For interactive applications this is usually sufficient, but there may be times when a higher resolution image is needed. Examples include color printing applications and computer graphics recorded for film. In these cases, higher resolution images can be divided into tiles that fit on the workstation's framebuffer. The image is rendered tile by tile, with the results saved into off screen memory, or perhaps a file. The image can then be sent to a printer or film recorder, or undergo further processing, such has downsampling to produce an antialiased image.

One straightforward way to tile an image is to manipulate the parameters to glFrustum(). The scene can be rendered repeatedly, one tile at a time, by changing the left, right, bottom and top arguments arguments of glFrustum() for each tile.

Computing the argument values is straightforward. Divide the original width and height range by the number of tiles horizontally and vertically, and use those values to parametrically find the left, right, top, and bottom values for each tile.

$$\begin{eqnarray*} tile(i, j); i : 0 \rightarrow nTiles_{horiz}, j : 0 \rightarr... ...ig} + \frac{top_{orig} - bottom_{orig}}{nTiles_{vert}} * j \\ \end{eqnarray*}$$

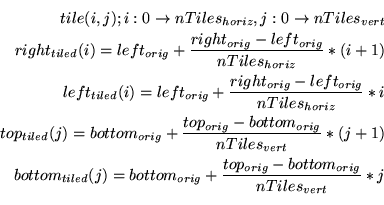
In the equations above, each value of $i$ and $j$ corresponds to a tile in the scene. If the original scene is divided into $nTiles_{horiz}$ by $nTiles_{vert}$ tiles, then iterating through the combinations of $i$ and $j$ generate the left, right top, and bottom values for glFrustum() to create the tile.

Since glFrustum() has a shearing component in the matrix, the tiles stitch together seamlessly to form the scene. Unfortunately, this technique would have to be modified for use with gluPerspective() or glOrtho(). There is a better approach, however. Instead of modifying the perspective transform call directly, apply transforms to the results. The area of normalized device coordinate (NDC) space corresponding to the tile of interest is translated and scaled so it fills the NDC cube. Working in NDC space instead of eye space makes finding the tiling transforms easier, and is independent of the type of projective transform.

Even though it is easy to visualize the operations happening in NDC space, conceptually, you can ``push'' the transforms back into eye space, and the technique maps into the glFrustum() approach described above.

For the transform operations to happen after the projection transform, the OpenGL calls must happen before it. Here is the sequence of operations:

glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glScalef(xScale, yScale);
glTranslatef(xOffset, yOffset, 0.f);
setProjection();

The scale factors xScale and yScale scale the tile of interest to fill the the entire scene:

$$\begin{eqnarray*} xScale &=& \frac{sceneWidth}{tileWidth} \\ yScale &=& \frac{sceneHeight}{tileHeight} \\ \end{eqnarray*}$$

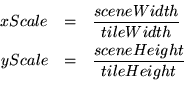
The offsets xOffset and yOffset are used to offset the tile so it is centered about the $z$ axis. In this example, the tiles are specified by their lower left corner relative to their position in the scene, but the translation needs to move the center of the tile into the origin of the $x$-$y$ plane in NDC space:

$$\begin{eqnarray*} xOffset = \frac{-2 * left}{sceneWidth} &+& (1 - \frac{1}{nTile... ...{-2 * bottom}{sceneHeight} &+& (1 - \frac{1}{nTiles_{vert}}) \\ \end{eqnarray*}$$

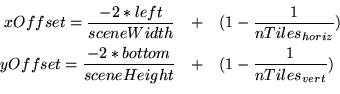
As before $nTiles_{horiz}$ is the number of tiles that span the scene horizontally, while $nTiles_{horiz}$ is the number of tiles that span the scene vertically.

Some care should be taken when computing $left$, $bottom$, $tileWidth$ and $tileHeight$ values. It is important that each tile is abutted properly with its neighbors. Ensure this by guarding against round-off errors. Some code that properly computes these values is given below:

    /* tileWidth and tileHeight are GLfloats */
    GLint bottom, top;
    GLint left, right;
    GLint width, height;
    for(j = 0; j < num_vertical_tiles; j++) {
            for(i = 0; i < num_horizontal_tiles; i++) {	
                    left = i * tileWidth;		
                    right = (i + 1) * tileWidth;		
                    bottom = j * tileHeight;		
                    top = (j + 1) * tileHeight;		
                    width = right - left;
                    height = top - bottom;
                    /* compute xScale, yScale, xOffset, yOffset */
            }
    }

Note that the parameter values are computed so that $left + tileWidth$ is guaranteed to be equal to $right$ and equal to $left$ of the next tile over, even if $tileWidth$ has a fractional component. If the frustum technique is used, similar precautions should be taken with the $left$, $right$, $bottom$, and $top$ parameters to glFrustum().