11.2.1.1 The Mathematics of Sphere Mapping

The vector from the eye point to the vertex is denoted as $\vec{U}$, normalized to $\vec{U'}$. Since the computation is performed in eye coordinates, the eye is located at the origin and $\vec{U}$ is equal to the location of the vertex in eye-space. The current normal $\vec{N}$ is transformed to eye coordinates by the inverse transpose of the modelview matrix and is normalized, becoming $\vec{N'}$. The reflected vector $\vec{R}$ can be computed as:

$$\vec{R} = \vec{U'} - 2(\vec{N'} \cdot \vec{U'})\vec{N'}$$ (7)

Define:

$$p = \sqrt{R^2_x + R^2_y + (R_z + 1)^2}$$

Then the texture coordinates are calculated as:

$$s = \frac{R_x}{2p} + \frac{1}{2}$$ (8)

$$t = \frac{R_y}{2p} + \frac{1}{2}$$ (9)

This computation happens internally to OpenGL in the texture coordinate generation step. The math is performed for each vertex of a primitive as shown in Figure 67.

The above equations look intimidating, but they are not as mystifying as they first appear. Equation 7 is the standard equation for computing the reflection vector given a surface normal and incident vector. Most introductory graphics textbooks have a short proof and a good explanation of this equation.⁹

Because $\vec{N'}$ and $\vec{U'}$ are normalized, $\vec{R}$ is normalized as well. You can think of $\vec{R}$ as a 3D point on the unit sphere. Our task is to make this 3D point into a 2D texture coordinate. Reducing to two dimensions is accomplished by projecting $\vec{R}$ onto the unit circle in the $R_z=0$ plane. This is the reason for dividing by $p$.

Because we know $\vec{R}$ is normalized, the result of $R_{x} / p$ and $R_{y} / p$ must be within the range $[-1,1]$. But to index into a 2D texture map, we need coordinates in the $[0,1]$ range. In Equations 8 and 9, the scale by $\frac{1}{2}$ and bias by $\frac{1}{2}$ serve to map values in the range the $[-1,1]$ to the range $[0,1]$.

When constructing sphere maps, the reverse mapping from $(s,t)$ to $\vec{R}$ is often needed. The reverse mapping is:

$$\begin{eqnarray*} R_{x} & = & 2 \sqrt{-4s^{2}+4s-1-4t^{2}+4t}(2t-1) \\ R_{y} & ... ...-4t^{2}+4t}(2s-1) \\ R_{z} & = & -8s^{2} + 8s - 8t^{2} + 8t - 3 \end{eqnarray*}$$

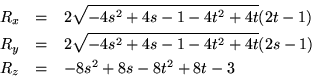
The image in a sphere map can be thought of as a circle of radius $\frac{1}{2}$ centered at $(\frac{1}{2},\frac{1}{2})$. Plugging $(\frac{1}{2},\frac{1}{2})$ into the reverse mapping equations above results in a reflection vector of $(0,0,1)$. OpenGL assumes the eye looks down the negative Z axis. So the vector $(0,0,1)$ is reflected straight back at the eye. If we think of a sphere map as what we see when looking directly at a chrome sphere, then dead in the center of the sphere we expect to see our own reflection.

Try plugging $(s,t)$ coordinates on the edge of the sphere map's circle such as $(0,\frac{1}{2})$ and $(\frac{1}{2},0)$ into the reverse mapping equations. For any point on the circle edge, the result is always $(0,0,-1)$. Again, if we think of a sphere map as what we see when looking at a chrome sphere, the silhouette edge of the sphere is seen as an extreme grazing reflection of whatever is directly behind the sphere. If this does not make sense, look back at Figure 66 to convince yourself of this fact. This means that every point on the circle's edge of a properly generated sphere map should the same color.

Finally try plugging $(s,t)$ coordinates for points outside the sphere map's circle into the reverse mapping equations. Try points such as $(0,0)$ and $(1,1)$. The operand of the square root in the equations for both $R_{x}$ and $R_{y}$ become negative. This should not be too surprising because properly normalized reflection vectors are guaranteed to fall within the sphere map's circle.